Gerrymandering Strategies

1: Introduction

Partisan gerrymandering is when a partisan draws legislative districts to maximize her party’s advantage in elections for the legislature ¹. In America, most districts are redrawn by incumbent legislators. Our focus is the theoretical literature concerning models and measures of gerrymandering. We will not discuss work on the effects of gerrymandering, and we will discuss empirical work only as it relates to measuring gerrymandering.

We are interested in learning what the best strategies for gerrymanderers are. If there were no uncertainty and the gerrymanderer could move people freely, her optimal move is to “pack” her opponents into districts where they win elections by large majorities and “crack” (spread) her support over a large number of districts where she would win elections by slim majorities. Does this result hold true as the model gets more realistic? To this end, we thoroughly review the major works in the economics literature that explicitly model gerrymandering as an optimization problem for a gerrymanderer. We find that there are broadly two classes of models: models that account for geography and models that do not. Among the models that do account for geography, the optimal strategy is to do a special form of packing and cracking called segregating and pairing: the gerrymanderer should pack her most vociferous opponents into homogeneous districts and pair all the other voters in a negatively assortative pattern. The optimal solution when geography is accounted for is not clear but it appears a simple pack and crack is not the answer.

We then review some measures of gerrymandering. Districts are strictly required to be contiguous and equally populated, but it is also desirable for districts to be compact and fair. Contiguity and population size are easily verifiable, but compactness and partisan fairness are much harder to measure. This makes detecting gerrymandering challenging. However, it is important to have measures of gerrymandering so model predictions can be compared.

For future research, we are interested in how optimal strategies from economic models might compare to optimal strategies from models that use computational approaches on the measures of gerrymandering we review. We also posit some possible extensions to the theoretical models of gerrymandering within economics.

In Section 2, we review models of gerrymandering within economics. In Section 3, we review measures of gerrymandering. In Section 4, we discuss avenues for future research. We conclude in Section 5.

2: Modelling Gerrymandering

2.1: The Very First Model

The earliest formal model of gerrymandering is from (Owen & Grofman, 1988). This seminal paper is a point of departure for almost all the work on modeling that has followed.

They assume the position of a partisan tasked with redistricting looking to maximize her party’s advantage subject to two constraints – districts must have equal populations and party support is fixed – and an exogenous probabilistic shock. There are two parties. They choose to ignore geographical constraints. There is some justification for this abstraction offered by (Sherstyuk, 1998): intuitively, since contiguity is the only unambiguously enforceable geographical constraint, the gerrymanderer can simply draw thin lines or wedges connecting otherwise disparate regions (see Figure 1). A lot of the literature has coalesced around this assumption. They also assume that support is homogenously distributed and equal for both parties. The exogenous shock is modeled by a random variable \(Z \sim H(Z)\) where \(H\) is known by the gerrymanderer. Every district, \(j\), the gerrymanderer draws is characterized by a support index \(\alpha_j \in [-1, 1]\). If \(\alpha_j > z\), then the gerrymander wins district \(j\). While they don’t explicitly use this language, one can think of \(\alpha_j\) as the median voter in the district. They consider two objective functions: expected vote share and the probability of winning control of the legislature. The optimal policy for both objective functions is the same: the gerrymanderer should pack and crack but allow for a bigger buffer in the cracked districts.

2.2: The Very First Model with Geography

(Sherstyuk, 1998) builds on the results in (Owen & Grofman, 1988) but expands on this work by explicitly modeling geography and the distribution of voter support for each of the two parties. They define a map \(M = \{A_{1}, \ldots, A_{k}\}\) as a Borel partition of a state \(B \subset \mathbb{R}^2\) into \(k\) subsets. A Borel partition satisfies:

1. The subsets belong to set: \(A_{i} \in B \ \forall i = 1 \ldots k\)
2. The subsets are disjoint: \(A_i \cap A_j=\emptyset \ \forall \mathrm{i} \neq \mathrm{j}, \mathrm{i}, \mathrm{j}=1, \ldots, \mathrm{k}\)
3. The union of the subsets forms the set: \(\bigcup_{i=1}^k A_i=B\)

These conditions intuitively apply to any valid redistricting scheme: all proposed districts must be a part of the state, cannot overlap, and their union should form the whole state. Next, every point \(x \in A_{i} \subset B\) has a time-variant party support index given by \(p_{t}(x) = p(x) +\epsilon_{t}\) where \(p(x)\) is a static measure of the gerrymanderer’s favorability at point \(x\) and \(\epsilon_{t}\) is an exogenous shock that swings voter preferences with some known distribution \(H(\epsilon)\). A voter located at \(x\) votes for the gerrymanderer’s party if \(p_{t}(x) \geq 0\). Additionally, the measure of voters in each district must be equal for a map to be valid: \(\mu(A_i) = 1/k \ \forall i=1, \ldots, k\).

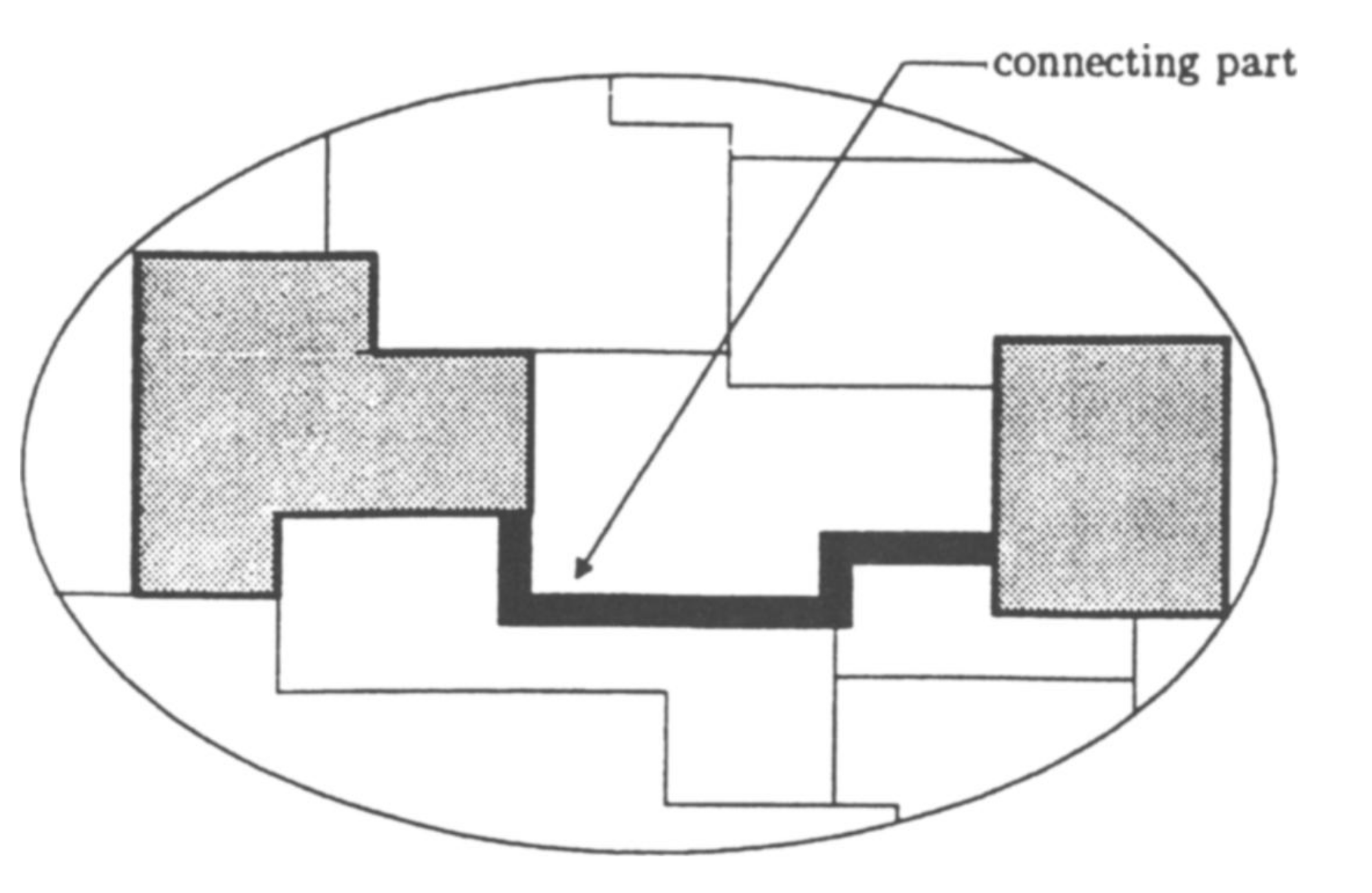
While they do not propose a general algorithm for how the gerrymanderer should draw the most partisan map, they prove that it becomes harder for the gerrymanderer to gerrymander as the distribution of party support becomes more evenly spread: if the gerrymanderer’s support is concentrated somewhere in B, it becomes easy to draw advantageous maps, but if instead it is evenly spread over B, the her advantage diminishes. They also show that while imposing constraints that force the mass of some communities of interest to be equal across districts makes gerrymandering more difficult, requiring districts to be contiguous does not. Two disparate regions can always be connected as shown in Figure 1.

2.3: Models with Micro-Foundations

Unlike (Owen & Grofman, 1988) and (Sherstyuk, 1998), (Friedman & Holden, 2008) build a micro-founded model where the gerrymanderer explicitly assigns specific voters to specific districts as opposed to just describing the properties of a redistricting plan. Like (Owen & Grofman, 1988), they choose not to model geography. A right-leaning gerrymanderer is faced with a unit mass of voters who offer noisy signals of their preferences over a one-dimensional policy space. Given this signal, she is able to compute the posterior distribution of preferences conditional on the signal from each voter. Her objective is to create N districts to maximize her party’s expected seat share given the conditional posterior she observes. However, the model is set up so that given a redistricting plan and the signals observed from voters, the policy preference of the median voter is uniquely identified – while there is uncertainty about who the median voter is, there is effectively no uncertainty about where the median voter lies. The uncertainty in this model is driven by an aggregate shock parameter with a known c.d.f. The micro-foundations in this model offer a more specific prediction than “packing and cracking with a buffer”: if the signal the gerrymandered receives is “high” quality, she should employ a “slice and mix” strategy grouping her most vociferous supporters and her most vociferous opponents. The signal is “high” quality if the voters’ true preferences are close to the observed signal. If the signal quality is low, then her optimal strategy is still to create “thicker slices” containing just her most ardent supporters. The intuition behind this result is that it is not optimal to create identical winning districts with the same winning median position because this wastes all of the voters who are to the right of that median.

(Friedman & Holden, 2020) extend the results from (Friedman & Holden, 2008) to a two-party, multi-state setting. In this extension, each party controls redirecting in a certain number of states but not others. They partially account for geography and contiguity by suggesting that instead of assigning individual voters, the gerrymanderers assign census blocks. The parties know the preferences of voters within blocks and thus know the median voters, and the median voters’ preferences in blocks and districts win. They find the same main result: the party in control groups the most extreme partisans into the same districts.

(Gul & Pesendorfer, 2010) build on (Friedman & Holden, 2008). In their model, they have two parties that control redistricting in some continuous mass of states where each party is attempting to maximize its probability of winning control in the House of Representatives. There are three sources of uncertainty in this model. The gerrymanderer observes a noisy signal of preferences. Unlike in (Friedman & Holden, 2008), the median voter’s position is not uniquely identified given a redistricting plan. There is an aggregate shock variable that causes party support to shift nationwide. Individual districts also experience local shocks that shift preferences locally – these can be interpreted as candidate quality shocks. The parties are assumed to draw maps prior to the aggregate uncertainty being resolved. They find that the solution for each party is to choose some cutoff based on the signal and pack opponents and crack support. (Gul & Pesendorfer, 2010) show that this difference in optimal strategy between their work and (Friedman & Holden, 2008) is driven by the differences in how the two works treat the information available to each party about voter preferences: if uncertainty about voter preferences is small as in (Friedman & Holden, 2008), the solution is to slice and mix, but if uncertainty about voter preferences is large, the solution is to pack and crack.

(Kolotilin & Wolitzky, 2020) reproduce the results from (Gul & Pesendorfer, 2010), (Friedman & Holden, 2008), and (Owen & Grofman, 1988) in a unified framework. They recast gerrymandering as an information design problem to draw on some of the results in that literature. In an information design problem, a designer “partitions the state of the world into signals, in order to induce a favorable reaction from the receiver” (p. 2). A partisan gerrymander draws equally-sized districts to cause her party to win the majority vote in the most districts possible (p. 2). Every voter has an observable type \(s \in [0, 1]\) that is subject to a taste shock \(r \in \mathbb{R}\) with some distribution \(G\). The joint distribution of \(s\) and \(r\) is given by \(v(s,r)\). The population of voter types is distributed according to \(F\). Without loss of generality, they assume that higher voters type support the gerrymander and higher realizations of the aggregate shock parameter favor the opposing party. The gerrymanderer chooses a voter distribution over types for each district, \(P \in \Delta[0,1]\). Choosing a redistricting plan is equivalent to choosing a distribution over districts, \(\mathcal{H} \in \Delta \Delta[0,1]\) subject to the distribution of s: \begin{equation} \int_P P d \mathcal{H}(P)=F \label{equality_constraint} \end{equation}

The gerrymanderer only wins districts in which she obtains a majority of the vote. Formally, she wins a district with a distribution \(P\) if \(\left\{r: \int v(s, r) d P(s) \geq 1 / 2\right\}\). The threshold for her to win a district with distribution \(P\), \(r^{*}(P)\), is defined as: \begin{equation} r^{*}(P)=\max \left\lbrace r: \int v(s, r) d P(s) \geq 1 / 2\right\rbrace \label{min_threshold} \end{equation}

The gerrymanderer has a utility scaling function \(W\) that depends on the total number of seats she wins given a redistricting plan \(\mathcal{H}\) and an aggregate uncertainty shock \(r \in G(R)\). She simply maximizes her expected utility as follows: \begin{equation} max_{\mathcal{H} \in \Delta \Delta[0,1]} \int_r W\left(\int_P \mathbf{1}\left\lbrace r \leq r^*(P)\right\rbrace d \mathcal{H}(P)\right) d G(r) \label{big_objective} \end{equation}

subject to constraints \(\eqref{equality_constraint}\) and \(\eqref{min_threshold}\).

(Kolotilin & Wolitzky, 2020) show that for (Gul & Pesendorfer, 2010), (Friedman & Holden, 2008), and (Owen & Grofman, 1988) are special cases of the maximization problem defined by \(\eqref{equality_constraint}\), \(\eqref{min_threshold}\), and \(\eqref{big_objective}\). They find that the optimal solution is a refinement of packing and cracking: the gerrymanderer should group “sufficiently” unfavorable voter types into homogeneous districts, and match all the other voter types in a negatively assortative manner. They call this approach “segregate and pair”. The strategies considered thus far are summarized in Figure 2. The simple “pack and crack” in (Owen & Grofman, 1988) is shown in Figure 2(a), the (Gul & Pesendorfer, 2010) “segregate and pair” approach is shown in Figure 2(b), the (Kolotilin & Wolitzky, 2020) the “segregate and pair” approach is in Figure 2(c), and the “pair” from (Friedman & Holden, 2008) is in Figure 2(d)². They find that under a variety of cases where there is a continuum of voters, these approaches are equivalently effective for the gerrymanderer. As uncertainty increases, they find the optimal solution converges to “segregate and pair”.

2.4: Endogenizing the Gerrymanderer’s Policy Preferences

(Gilligan & Matsusaka, 2006) endogenize the policy preferences of the gerrymanderer. There are \(N\) voters who must be divided into \(K\) equal-sized districts and have policy preferences \(x \in \mathbb{R}\). They assume the gerrymander has the most extreme policy position. Each district is won by a candidate representing the median voter of that district, denoted \({x^*}_{k}\). The policy position of the median voter in the state is denoted \(x^*_{POP}\). The policy passed in the legislature is \(x^*_{LEG}\) = median(\({x^*_{1} \ldots x^*_{k} \ldots x^*_{K}}\)). The gerrymanderer’s objective is to maximize bias towards her view where bias is defined as \(B = |F(x^*_{LEG}) - F(x^*_{POP})|\). Since the model has no uncertainty or geography, the optimal strategy for their gerrymanderer is to pack and crack. Their model’s contribution is to show that the maximum attainable bias for an extreme gerrymanderer is increasing in the population, \(N\).

(Konishi & Pan, 2020) introduce a model where the gerrymanderer is both policy-motivated and office-motivated. The gerrymanderer who has some policy preferences drawn from a one-dimensional policy space competes with representatives to pass her most favored policy in exchange for “pork-barrel” promises. It is expensive for the gerrymanderer to woo party members whose policy preferences differ massively from hers. (Konishi & Pan, 2020) find that if the gerrymanderer has to abide by the implicit constraint in (Owen & Grofman, 1988) that the average of the median voters across districts must be the same before and after redistricting, the solution is to pack her most ardent opponents into districts she cannot win, and slice (but not mix) the remaining districts consecutively. They call this “order and partition”. If this constant-average-median constraint is relaxed, they find the gerrymanderer’s best move is to “slice and mix” as in (Friedman & Holden, 2008).

2.5: Other Models With Geography

Some other approaches have been taken in the literature to model geography and contiguity in more tractable ways. (Shotts, 2001) produce a model similar to the (Owen & Grofman, 1988) model but with what they call “minimum density constraints.” These are just minimums on the number of Democrats, minority Democrats, and Republicans each district must contain³.In the words of (Friedman & Holden, 2008), this is a “reduced-form” way of modeling geography and contiguity. More recent papers including (Friedman & Holden, 2020), (Konishi & Pan, 2020), and (Kolotilin & Wolitzky, 2020) loosely account for geography and contiguity by recasting the gerrymanderer’s problem as allocating a very large number of small groups of voters such as census tracts or voting blocks as opposed to allocating individual voters to districts. I would describe this approach as reduced-form as well.

(Puppe & Tasnádi, 2009) build a model with geography but without uncertainty. They have two parties, a set of voters \(N\) indexed by \(n\), and a set of districts \(\mathcal{D}\) indexed by \(d\). Voters have observable preferences \(v: N \rightarrow\{A, B\}\), and these preferences determine the number of votes for each party. A geography is a subset \(\mathcal{S} \subset 2^N\) such that all the elements of \(\mathcal{S}\) are (i) equally sized and (ii) partition N. A redistricting plan given \((N, \mathcal{S})\) is a mapping \(f: N \rightarrow \mathcal{D}\) such that \(f^{-1}(i) \in \mathcal{S}\) for all \(\mathrm{i} \in \mathcal{D}\) and \(\cup_{i \in \mathcal{D}} f^{-1}(i)=N\). A weakness here is that they cannot define a notion of contiguity in this setting. However, they do show by counterexample that the “pack and crack” strategy can be sub-optimal even in the absence of any uncertainty if geography is accounted for.

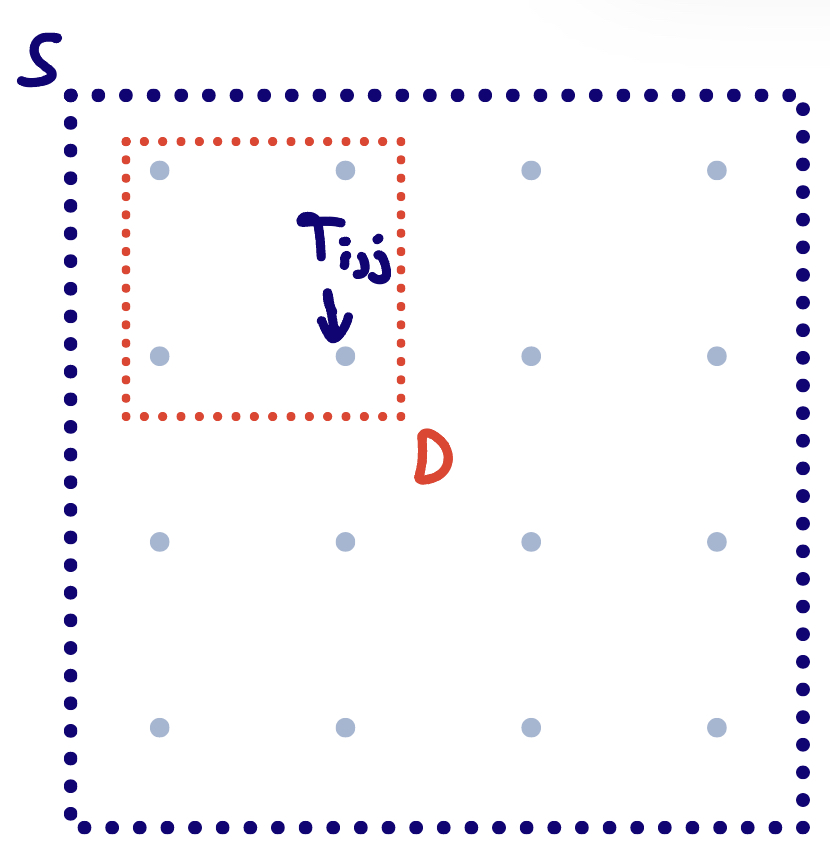
(Gatesman & Unwin, 2021) choose to model the problem as a gerrymanderer partitioning a two-dimensional lattice. A two-dimensional lattice is a discrete subset of \(\mathbb{R}^2\) that is closed under addition and subtraction ⁴. This can be visualized as shown in Figure 3. One can interpret every grey dot as a voter or more realistically as a voting unit of some kind indexed by \(T_{i,j}\) and a state, \(S\), as a collection of such units. Every unit \(T_{i,j}\) has an associated population \(P_{i, j} \in \mathbb{N}\) and a voting preference parameter \(v_{i, j} \in (-1,1)\). The total population of the \(S\) is defined as \(P_S=\sum_{i, j} P_{i, j}\). Given a territory \(S\), a district \(D\) is a finite union of voting units, \(D=\cup_{(i, j) \in I} T_{i, j}\) for an index set \(I\), and the district population is defined as \(P_D=\sum_{(i, j) \in I} P_{i, j}\). Not only does this representation allow for modeling party support and uncertainty, but it also offers natural definitions of adjacency between voting units and the contiguity of districts. They use simulation to test the results from (Friedman & Holden, 2008) in their lattice setting. They find that the “slice and mix” approach is not optimal for the gerrymanderer.

3: Measuring Gerrymandering

3.1: Measuring Compactness

Compactness is hard to define. As pointed out by (Schutzman, 2020), it is if nothing else a neutral measure in a procedural sense, and it is a characteristic that the gerrymandering literature and courts care about⁵. Adopting a distinction drawn by (Young, 1988), the compactness of a district and the compactness of a redistricting plan are two separate criteria. However, the former seems to receive more attention. In describing measures of district compactness, we adopt the taxonomy used by (Chambers, 2010): measures of district compactness are either interested in dispersion or the perimeter of the districts drawn. A lot of dispersion is considered undesirable as are large perimeters.

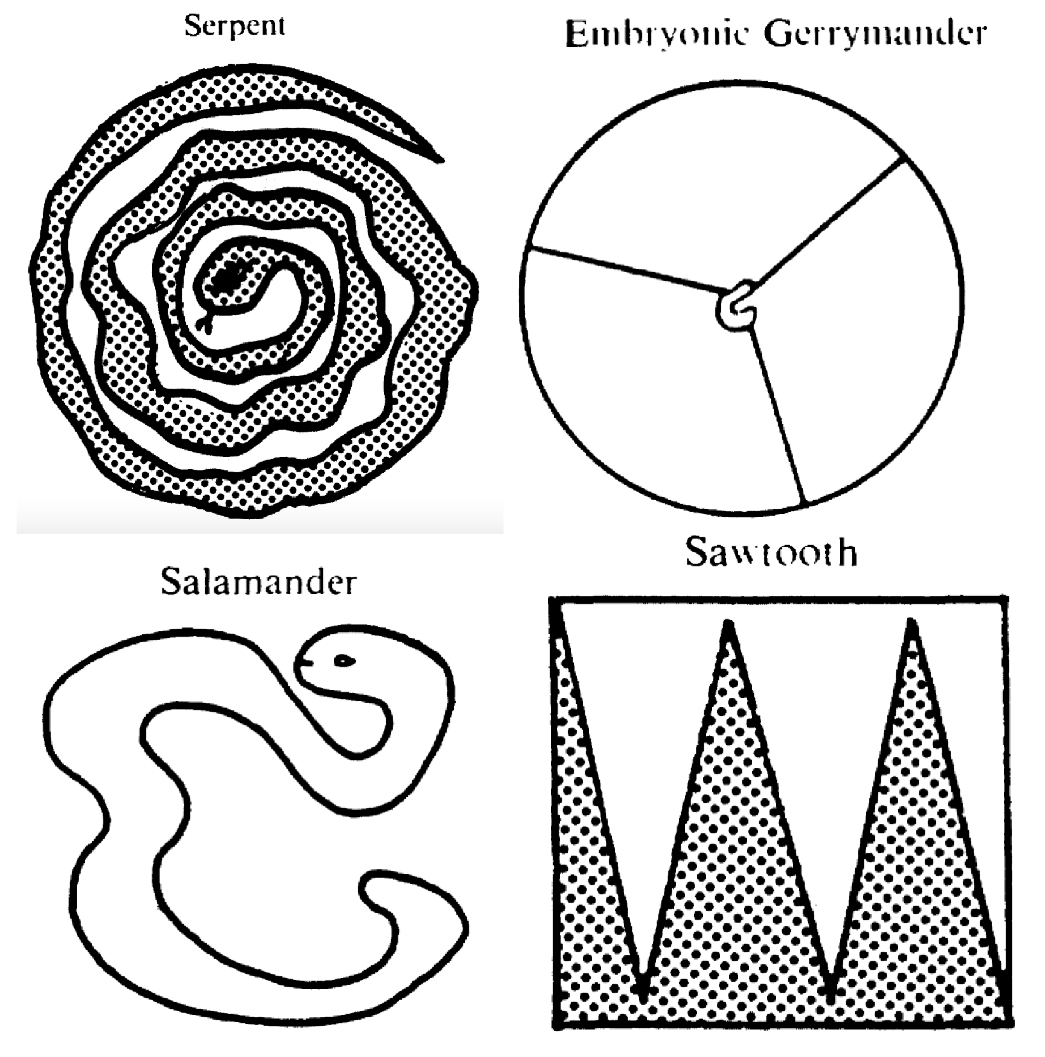
(Reock, 1961) proposed a test where the area of a district is compared to the area of the smallest possible circle that could contain that district. As pointed out by (Young, 1988), under this metric serpentine districts such as the one drawn in Figure 4 would be acceptable. The convex hull test, which compares the area of the convex hull containing the district to the area of the district, would also not objects to the serpentine district in Figure 4. (Schwartzberg, 1965) proposed a test that compares the perimeter of a district to the circumference of a circle whose area is equal to the area of the district. (Young, 1988) point out that this measure is very sensitive to small distortions on the boundaries. The length-width test compares the length and width of the smallest possible rectangle that can contain a district. The salamander district in Figure 4 as pointed out by (Young, 1988) would receive a near-perfect compactness score because it can be roughly encompassed in a square. Additionally, the length-width test would be indifferent between the two saw-tooth districts in Figure 4 and the two triangular districts that would result from cutting diagonally across the rectangle containing the saw-tooth districts.

The perimeter test assesses a redistricting plan as opposed to a district: add up the perimeters of all the districts in a plan – the smaller this sum, the more compact the districts. (Young, 1988) points out that in a state where the population is very densely packed around the center, this metric would prefer the “embryonic gerrymander” in Figure 4 compact over a plan that splits this state into four equal quadrants.

There are several other such tests documented and critiqued in (Young, 1988) and also in (Niemi et al., 1990)⁶. (Young, 1988) shows that the thresholds that have been suggested for most measures of compactness are often not very good, and suggests that it might be worth doing away with trying to “measure” compactness altogether. (Niemi et al., 1990) suggest using a combination of measures as opposed to any single measure, but this remains subjective. In fact, after reading (Young, 1988), one might be tempted to think that for any conceivable district, there exists a corresponding measure of compactness that does not find it objectionable. Nonetheless, compactness remains popular in the literature as a characteristic to at least comment on. This is particularly true in work that examines computational approaches to redistricting: see (Gatesman & Unwin, 2021), (Guest et al., 2019), (Levin & Friedler, 2019), (Mehrotra et al., 1998), (Altman & McDonald, 2018). More recently (Kaufman et al., 2021) used data from a large survey where respondents were asked to rank districts in order of compactness to train a model that is more predictive than the measures discussed so far; this approach seems very promising.

3.2: Measuring Partisan Fairness

It is worth drawing a distinction between procedural fairness and fairness of outcomes. This distinction is drawn in (Katz et al., 2020) and (Schutzman, 2020). For example, random redistricting may be procedurally fair but may result in maps that unfairly favor one party as shown in (Gilligan & Matsusaka, 2006). Similarly, (Chen, 2013) show that maps drawn by neutral bodies also can result in unfair outcomes. Neither is desirable. With good reason, the literature is more concerned with measures of fairness of outcomes and so I will focus on those in this section.

As stated by (Katz et al., 2020), partisan symmetry is an important standard of fairness. Intuitively, if Republicans win y% of the seats in the legislature with x% of the popular vote, then Democrats should also win y% of the seats in the legislature with x% of the popular vote. In the notation of (Katz et al., 2020), let \(S(V)\) be the seat share won by a party with \(V\) share of the popular vote; Partisan symmetry is satisfied if \(S(V) = 1 - S(1-V)\) holds, and bias is a measure of deviation from symmetry: \(\beta(V)=\frac{\{S(V)-[1- S(1-V)]\}}{2}\) \(\forall V \in[0,1]\). If Democrats need more than 50% of the vote to win 50% of the seats while Republicans need less than 50% of the vote to win 50% of the seats, then a map is biased.

The seat-vote curve introduced by (Browning & King, 1987) illustrates both symmetry and bias for a given map. It is a key diagnostic tool in the empirical literature that attempts to detect partisan gerrymandering and the literature that draws optimal maps. For example, (Coate & Knight, 2007) compare socially optimal seat-vote curves to observed seat-vote curves for every state and show how deviations relate to welfare losses. Figure 5, borrowed from (Katz et al., 2020), shows several examples.

Figure 5(a) shows three symmetric (and thus bias-free) curves with different degrees of responsiveness. Responsiveness is how much the state-wide seat share is affected by a marginal increase in state-wide vote share – it is simply the slope of the seat-vote curve. In a majoritarian system with multiple districts, one would expect a large gain in seat share in around the 50% vote share threshold, but that gain diminishes moving away from the threshold. For example, winning an additional 2% vote share at 50% of the vote share will result in a larger gain in seat share than a 2% gain at 80% of the vote share. This corresponds to the blue line in Figure 5(a).

Figure 5(b) represents a system where the seats are allocated proportionally, so responsiveness is one. Figure 5(c) represents a winner-take-all system where the party with marginally over 50% of the vote wins all the seats. Responsiveness is zero everywhere except at 50%. The blue curve and the red curve in Figure 5(b) are asymmetric and biased. Several other measures of partisan bias are derived from various features of the seat-vote curve. For example, the deviation of the observed seat-vote curve from the proportional seat-vote curve is sometimes of interest; a value close to zero is desirable but is structurally unlikely in a majoritarian system. See (Nagle, 2015) and (Katz et al., 2020) for a full discussion.

Seat-vote curves need to be empirically estimated using past election results. The original approach in (Browning & King, 1987) assumes that the seat-vote curve has the following functional form:

\begin{equation} \frac{S}{1-S}=\beta\left(\frac{V}{1-V}\right)^\rho \label{sv_equation} \end{equation}

where \(\beta\) is the bias parameter and \(\rho\) is the responsiveness parameter. These parameters can then be estimated using past election results. A limitation is that since maps change every 10 years, there are at most five data points for a given map. However, they assume that \(\beta\) and \(\rho\) do not vary much over time in a given state so they can use older election results as well. (Katz et al., 2020) offer a discussion of additional assumptions that can be made to use more data and some non-parametric approaches as well.

The efficiency gap is a popular measure of partisan fairness proposed by (Stephanopoulos & McGhee, 2014) that does not depend on the seat-vote curve. Formally, it is defined in the notation of (Bernstein & Duchin, 2017) as follows: \begin{equation} E G=\sum_{i=1}^S \frac{W_i^D-W_i^R}{T}=\frac{W^D-W^R}{T} \label{eq:refname} \end{equation} where \(W^D\) and \(W^R\) are the votes wasted by each party in a state-wide election. Votes are wasted if they do not materially change the outcome of a district race: any votes cast for a losing candidate in a district are wasted and any votes cast in excess of the winning threshold (over 50%) are also wasted. The intuition is that if the efficiency gap is close to zero, any packing and cracking effectively cancels out. (Bernstein & Duchin, 2017) point out several shortcomings of this measure. It penalizes representative districts in states where the partisan split is skewed. It also penalizes competitive races as they have lop-sided vote wastage which makes fair, competitive districts appear gerrymandered. The efficiency gap also has poor edge performance: it does not work well when the number of districts in a state is small and when party support is very skewed (in excess of 80-20 splits). A similar critique is offered by (Katz et al., 2020) as well.

The mean-median measure is another measure agnostic of the seat-vote curve. It is the difference between the average district vote and the median district vote. A lower score is desirable. Several measures that are similarly unrelated to the seat-vote curve exist and are detailed in (Katz et al., 2020).

4: Future Research

4.1: Theoretical Extensions

Of the models discussed in Section 2, a possible extension is voters moving away from the districts in which they are grouped. Since maps are drawn every ten years and new maps take effect two years after they are drawn, voters observe what district they have been placed into before they actually have to vote. It seems unlikely that voters will see they have been gerrymandered into a packed district and then decide to move to a cracked district to advantage their party right away, but over five election cycles, voters might move for a variety of other reasons. Alternatively, an exogenous shock might cause certain types of voters to move disproportionately. For example, a pandemic that alters attitudes toward working remotely might cause urban workers who tend to be more liberal to move away in search of cheaper housing. Such migration patterns might dampen the gerrymanderer’s advantage.

The literature has also mostly steered away from dealing explicitly with geographical constraints. While there is some theoretical justification for this in (Sherstyuk, 1998), the results from models without geography need not apply to models with geography as shown by counterexample by (Puppe & Tasnádi, 2009). Solving models with geography and uncertainty remains undone. As a first step, it is worth testing if the “segregate and pair” approach (Kolotilin & Wolitzky, 2020) can be proven sub-optimal (possibly by counterexample).

4.2: Linking Economic Theory With Computational Approaches From Other Fields

Since gerrymandering is studied by a wide range of researchers from different fields, there is the potential to integrate the approaches from other disciplines into the models and measures of gerrymandering in economics. For example, (Gatesman & Unwin, 2021) simulate the strategy proposed by (Friedman & Holden, 2008) on their lattice model and find that the resulting maps are highly disconnected. When they impose contiguity on slicing and mixing, they find that the gerrymanderer can do better by using what they call a “genetic gerrymandering” approach. The basic algorithm is that the gerrymander chooses some initial map and then tries to choose a better map based on some improvement criteria. This approach is borrowed from computational biology. One immediate next step might be to test the “segregate and pair” approach against this particular algorithm. There are other algorithmic approaches as well. For example, in (Guest et al., 2019), a social planner maximizes compactness subject to an equality constraint using clustering. This approach could be applied to a model where a gerrymanderer maximizes some partisan objective instead. There are some other works on optimal redistricting that use algorithmic approaches that can be modified to the partisan gerrymanderer setting. In fact, (Gatesman & Unwin, 2021) modify earlier work that used genetic mutation algorithms for socially optimal redistricting. (Levin & Friedler, 2019) and (Ito et al., 2021) use graph partitioning methods that could be promising.

(Katz et al., 2020) use a classification model based on survey respondents to predict compactness, it might be possible to build a similar model of partisan fairness. We concede that compactness is more of a “you know it when you see it” property than partisan fairness, but measures of partisan fairness are not perfect either. One could imagine doing a survey where respondents are given a series of stylized facts about some number of districts and asked to rank the results in order of fairness. This could result in a more nuanced understanding of what voters actually consider fair.

Lastly, using simulation methods can uncover relationships that might not be readily apparent otherwise or be difficult to definitively prove. For example, (Schutzman, 2020) simulates a set of redistricting plans optimizing for compactness and another set of redistricting plans optimizing for partisan fairness and finds that there is a trade-off. There are tools to make this type of research more accessible. For example, (GerryChain, 2022) is an open-source software package that can be used to simulate maps.

5: Conclusion

We have thoroughly reviewed the literature that explicitly models partisan gerrymandering. Most models ignore geographical constraints and find that the optimal policy for a gerrymanderer facing uncertainty is to do a special form of packing and cracking called segregating and pairing: the gerrymanderer should pack her most vociferous opponents into homogeneous districts and pair all the other voters in a negatively assortative pattern. The optimal solution in models that do explicitly model geography is much less clear, but it appears a simple pack and crack is not the answer. Simulation results show that applying the results from models without geography to models where geography is accounted for and thus contiguity is imposed can lead to districts that are both sub-optimal from a partisan perspective and very irregularly shaped.

We have also considered some measures of gerrymandering. Districts must be contiguous and equally populated, but “good” districts should also be compact and fair. Compactness is a slightly nebulous concept that is hard to measure but it is often reported on and weakly required by courts. Partisan fairness is most often associated with partisan symmetry and bias. Seat-vote curves capture partisan symmetry and bias and are standard diagnostic tools in the literature. While these and more measures exist, precisely identifying and quantifying gerrymandering remains contentious.

In terms of future research, there are still many theoretical extensions that are possible, especially solving models with geography, or at least testing more theories from models without geography on models with geography. More bridges can be drawn between the results from economic theory and the results from computational approaches. In particular, simulation techniques can be used to compare different optimal policies from economic models to optimal policies proposed by different algorithms.

References

1. Owen, G., & Grofman, B. (1988). Optimal partisan gerrymandering. Political Geography Quarterly, 7(1), 5–22. https://doi.org/10.1016/0260-9827(88)90032-8
2. Young, H. P. (1988). Measuring the Compactness of Legislative Districts. Legislative Studies Quarterly, 13(1), 105–115. https://doi.org/10.2307/439947
3. Sherstyuk, K. (1998). How to Gerrymander: A Formal Analysis. Public Choice, 95(1/2), 27–49. https://www.jstor.org/stable/30024359
4. Mehrotra, A., Johnson, E. L., & Nemhauser, G. L. (1998). An Optimization Based Heuristic for Political Districting. Management Science, 44(8), 1100–1114. https://www.jstor.org/stable/2634689
5. Shotts, K. W. (2001). The Effect of Majority-Minority Mandates on Partisan Gerrymandering. American Journal of Political Science, 45(1), 120–135. https://doi.org/10.2307/2669363
6. Gilligan, T. W., & Matsusaka, J. G. (2006). Public Choice Principles of Redistricting. Public Choice, 129(3/4), 381–398. https://www.jstor.org/stable/25487604
7. Coate, S., & Knight, B. (2007). Socially Optimal Districting: A Theoretical and Empirical Exploration. The Quarterly Journal of Economics, 122(4), 1409–1471. https://www.jstor.org/stable/25098880
8. Friedman, J. N., & Holden, R. T. (2008). Optimal Gerrymandering: Sometimes Pack, but Never Crack. The American Economic Review, 98(1), 113–144. https://www.jstor.org/stable/29729966
9. Gul, F., & Pesendorfer, W. (2010). Strategic Redistricting. American Economic Review, 100(4), 1616–1641. https://doi.org/10.1257/aer.100.4.1616
10. Bracco, E. (2013). Optimal districting with endogenous party platforms. Journal of Public Economics, 104, 1–13. https://doi.org/10.1016/j.jpubeco.2013.04.008
11. Levin, H. A., & Friedler, S. A. (2019). Automated Congressional Redistricting. ACM Journal of Experimental Algorithmics, 24, 1–24. https://doi.org/10.1145/3316513
12. Guest, O., Kanayet, F. J., & Love, B. C. (2019). Gerrymandering and computational redistricting. Journal of Computational Social Science, 2(2), 119–131. https://doi.org/10.1007/s42001-019-00053-9
13. Schutzman, Z. (2020). Trade-offs in Fair Redistricting. Proceedings of the AAAI/ACM Conference on AI, Ethics, and Society, 159–165. https://doi.org/10.1145/3375627.3375802
14. Konishi, H., & Pan, C. Y. (2020). Partisan and bipartisan gerrymandering. Journal of Public Economic Theory, 22(5), 1183–1212. https://doi.org/10.1111/jpet.12433
15. Ito, T., Kamiyama, N., Kobayashi, Y., & Okamoto, Y. (2021). Algorithms for gerrymandering over graphs. Theoretical Computer Science, 868, 30–45. https://doi.org/10.1016/j.tcs.2021.03.037
16. Gatesman, K., & Unwin, J. (2021). Lattice Studies of Gerrymandering Strategies. Political Analysis, 29(2), 167–192. https://doi.org/10.1017/pan.2020.22
17. Gilligan, T. W., & Matsusaka, J. G. (1999). Structural Constraints on Partisan Bias under the Efficient Gerrymander. Public Choice, 100(1/2), 65–84. https://www.jstor.org/stable/30026080
18. Friedman, J. N., & Holden, R. (2020). Optimal Gerrymandering in a competitive environment. Economic Theory Bulletin, 8(2), 347–367. https://doi.org/10.1007/s40505-020-00188-3
19. Kolotilin, A., & Wolitzky, A. (2020). The Economics of Partisan Gerrymandering [SSRN Scholarly Paper]. https://doi.org/10.2139/ssrn.3698690
20. Cox, G. W., & Katz, J. N. (1999). The Reapportionment Revolution and Bias in U. S. Congressional Elections. American Journal of Political Science, 43(3), 812–841. https://doi.org/10.2307/2991836
21. Cox, J. N. (2002). Elbridge Gerry’s salamander : the electoral consequences of the reapportionment revolution. Cambridge University Press.
22. Bernstein, M., & Duchin, M. (2017). A Formula Goes to Court: Partisan Gerrymandering and the Efficiency Gap. Notices of the American Mathematical Society, 64(09), 1020–1024. https://doi.org/10.1090/noti1573
23. Puppe, C., & Tasnádi, A. (2009). Optimal redistricting under geographical constraints: Why “pack and crack” does not work. Economics Letters, 105(1), 93–96. https://doi.org/10.1016/j.econlet.2009.06.008
24. Measuring Compactness. Retrieved November 13, 2022, from https://fisherzachary.github.io/public/r-output.html
25. Gill, B. R. Supreme Court of the United States (p. 48).
26. Nagle, J. F. (2015). Measures of Partisan Bias for Legislating Fair Elections. Election Law Journal: Rules, Politics, and Policy, 14(4), 346–360. https://doi.org/10.1089/elj.2015.0311
27. Grofman, B., & King, G. (2007). The Future of Partisan Symmetry as a Judicial Test for Partisan Gerrymandering after \textitLULAC v. Perry. Election Law Journal: Rules, Politics, and Policy, 6(1), 2–35. https://doi.org/10.1089/elj.2006.6002
28. Stephanopoulos, N. O., & McGhee, E. M. (2014). Partisan Gerrymandering and the Efficiency Gap. The University of Chicago Law Review, 70.
29. Browning, R. X., & King, G. (1987). Seats, Votes, and Gerrymandering: Estimating Representation and Bias in State Legislative Redistricting. Law & Policy, 9(3), 305–322. https://doi.org/10.1111/j.1467-9930.1987.tb00413.x
30. Chambers, C. P. (2010). A Measure of Bizarreness. Quarterly Journal of Political Science, 5(1), 27–44. https://doi.org/10.1561/100.00009022
31. Reock, E. C. (1961). A Note: Measuring Compactness as a Requirement of Legislative Apportionment. Midwest Journal of Political Science, 5(1), 70–74. https://doi.org/10.2307/2109043
32. Schwartzberg, J. E. (1965). Reapportionment, Gerrymanders, and the Notion of Compactness. Minnesota Law Review, 50(3), 443–452. https://heinonline.org/HOL/P?h=hein.journals/mnlr50&i=459
33. Niemi, R. G., Grofman, B., Carlucci, C., & Hofeller, T. (1990). Measuring Compactness and the Role of a Compactness Standard in a Test for Partisan and Racial Gerrymandering. The Journal of Politics, 52(4), 1155–1181. https://doi.org/10.2307/2131686
34. Altman, M., & McDonald, M. (2018). Redistricting by Formula: An Ohio Reform Experiment. American Politics Research, 46(1), 103–131. https://doi.org/10.1177/1532673X17700611
35. Katz, J. N., King, G., & Rosenblatt, E. (2020). Theoretical Foundations and Empirical Evaluations of Partisan Fairness in District-Based Democracies. American Political Science Review, 114(1), 164–178. https://doi.org/10.1017/S000305541900056X
36. Kaufman, A. R., King, G., & Komisarchik, M. (2021). How to Measure Legislative District Compactness If You Only Know It When You See It. American Journal of Political Science, 65(3), 533–550. https://doi.org/10.1111/ajps.12603
37. Chen, J. (2013). Unintentional Gerrymandering: Political Geography and Electoral Bias in Legislatures. Quarterly Journal of Political Science, 8(3), 239–269. https://doi.org/10.1561/100.00012033
38. Gelman, A., & King, G. (1994). A Unified Method of Evaluating Electoral Systems and Redistricting Plans. American Journal of Political Science, 38(2), 514–554. https://doi.org/10.2307/2111417
39. GerryChain. (2022). Metric Geometry and Gerrymandering Group. https://github.com/mggg/GerryChain
40. Abramowitz, A., Alexander, B., & Gunning, M. (2006). Don’t Blame Redistricting for Uncompetitive Elections. PS: Political Science and Politics, 39(1), 87–90. http://www.jstor.org/stable/20451683
41. Stephanopoulos, N. The Causes and Consequences of Gerrymandering. 59.

Footnotes